The (Micro) Genetic Algorithm - generally and specifically

Apr 22, 2023

What is the Genetic Algorithm?

The genetic algorithm is a method for solving optimization problems that is based on natural selection. The genetic algorithm repeatedly improves a population of individuals. At each iteration, the GA selects parents from the current population of individuals (ranking), which then produce the children for the next generation (breeding). Over many generations, the population converges to an optimal solution by replacing the weakest individuals by the children.

This process can be easily described using the following pseudocode:

create population
while (stopping criteria not met)
  select parents from population
  generate children
  replace worst individual with child in the population
extract the best individual

To summarize: Population is the set of all the individuals (also called chromosomes). Each chromosome carries some information about itself stored and segmented into genes.

There are four critical parts of the algorithm and many different methods of how to approach them. Let's take a look at some of them and see how the (Micro) GA can be implemented on a high level. I will use this implementation as a base to our concrete problem later on.

Aspects of the algorithm and basic implementation

1. Encoding

The representation of the population in the algorithm. This might be:

• Binary/Octal/Hexadecimal Encoding
• Permutation Encoding
Having a predefined set of genes, each chromosome is a permutation of this set and each gene is represented at most once.
• Value Encoding
Genes simply represent the specific value.
• Tree Encoding
Usually used to encode programs or expression. Representation of objects, where order is important.

For example implementation of a random population of $N$ individuals $p_n$, where $p_n$ is a bitstring of length $L$, would look like this:

public Population(int size) {
    individuals = new Chromosome[size];
    random = new Random();
    for (int i = 0; i < size; i++) {
        int[] genes = new int[10];
        for (int j = 0; j < genes.length; j++) {
            genes[j] = random.nextInt(2);
        }
        individuals[i] = new Chromosome(genes);
    }
}

2. Fitness Function & Parents Selection

This determines how the parents of the next-generation children are selected. Evaluation (ranking) of potential parents is done by the fitness function. This is the metric the GA tries to optimize.
For the example we had before, we choose our fitness function as the sum of the bits in a chromosome: $$ F(p_n) = \sum_{i = 0}^{L-1} p_{n_i} \quad \text{where } p_{n_i} \text{ is the i-th bit in } p_n $$ Based on the fitness function, these are some usual methods to select parents:

• Tournament Selection
Choosing $n$ individuals randomly and selecting the best one among them.
• Rank Selection
Sort candidate chromosomes by their fitness value. These ranks will be used in a roulette wheel style selection.
• Roulette Wheel Selection
Let $S$ be a sum of the fitness function for all candidate chromosomes and $r \in [0,S]$ randomly generated number. Then iterate throught candidates and compute the sum of their fitness. Choose the candidate for which the sum $=r$ was achieved.

For our purposes, the tournament selection will do just fine. To choose one parent, we randomly choose $n = 5$ individuals from the population and select the one with the highest fitness function.

public Chromosome select() {
Chromosome best = null;
for (int i = 0; i < 5; i++) {
    Chromosome individual = individuals[random.nextInt(individuals.length)];
    if (best == null || individual.getFitness() > best.getFitness()) {
        best = individual;
    }
}
return best;
}

We actually call this function twice to generate two parents on which we then perform the crossover. In the main iteration loop, this will look like this:

// Select parents
Chromosome parent1 = population.select();
Chromosome parent2 = population.select();

// Crossover
Chromosome[] children = parent1.crossover(parent2);

3. Crossover

Crossover specifies how the algorithm combines the parents to obtain the children.

• Single/Multi-Point Crossover
We choose a point $k \in [1,n-1]$ where $n$ is number of genes and we mix the parents at this midpoint to obtain the children (offspring). For multi-point crossover just assume mulitple "midpoints".

Single-Point Crossover
• Uniform Crossover
This is a generalization of the multi-point crossover. Assume a bitmask with the same length as the parents chromosomes. A $1$ in the bitmask on the position $p$ can represent that the $p$-th bit in the first child will be inherited from the first parent and in the second child from the second parent and vice versa for bit 0 in the bitmask.
• and other like Partially Mapped Crossover, Order Crossover, Shuffle Crossover...

We choose to implement one-point crossover, i.e. randomly generate a midpoint $\in [0;L]$ and generate child by taking bits from $0$ to $midpoint$ from parent1 and the rest from parent2.

public Chromosome[] crossover(Chromosome other) {
  int[] childGenes = new int[genes.length];
  int[] otherChildGenes = new int[genes.length];
  int midpoint = random.nextInt(genes.length);
  
  for (int i = 0; i < midpoint; i++) {
      childGenes[i] = genes[i];
      otherChildGenes[i] = other.genes[i];
  }
  for (int i = midpoint; i < genes.length; i++) {
    childGenes[i] = other.genes[i];
    otherChildGenes[i] = genes[i];
  }
  
  Chromosome first_child = new Chromosome(childGenes);
  Chromosome second_child = new Chromosome(otherChildGenes);
  Chromosome[] children = {child1, child2};
  
  return children;
}

We then replace this new child with the weakest individual (individual) with the lowest fitness function.

public void replaceWorst(Chromosome child) {
int worstIndex = 0;
double worstFitness = Double.MAX_VALUE;
for (int i = 0; i < individuals.length; i++) {
    if (individuals[i].getFitness() < worstFitness) {
        worstIndex = i;
        worstFitness = individuals[i].getFitness();
    }
}
individuals[worstIndex] = child;
}

4. Mutation

Serves to preserve randomness and diversity of the children. For binary encoding, common mutation techniques are:

• Bit-Flipping Mutation
Randomly flip bits in the parents to obtain children.
• Swap Mutation
Swap some parent-bits.
• Inversion Mutation
Inverse some parent-bits.

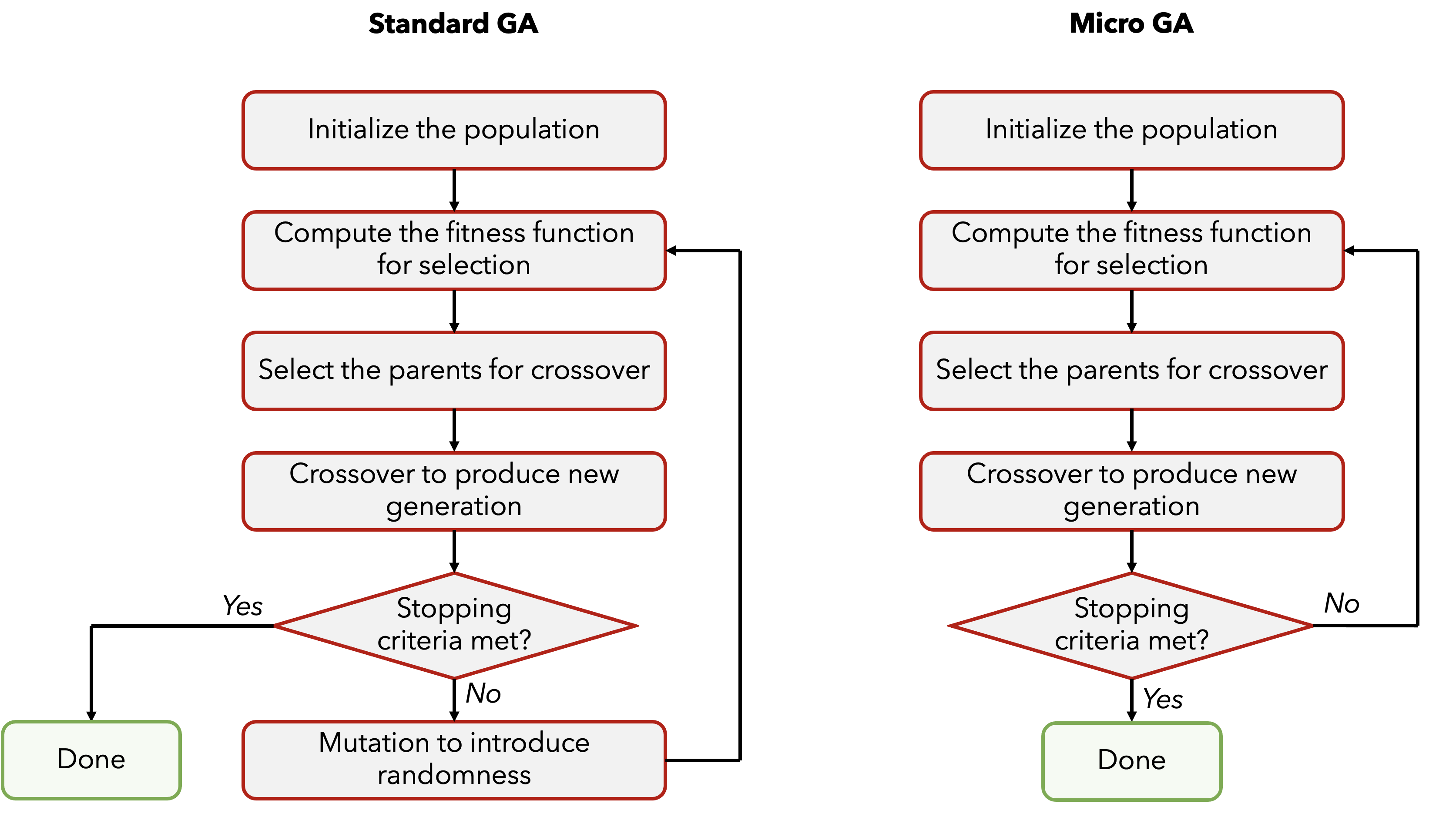
For a real-value encoding, one approach is to add a random value $m$ to the original value $x$, which results in a mutated value $$ x' = x + m $$ If a given to-be-mutated gene is restricted by some range of values, make sure the mutated value is again in this range. Sometimes, it might make sense to omit the mutation step. If we do so, such algorithm is then called Micro Genetic Algorithm.

5. Stopping Criteria

As seen in the flowchart above, stopping criteria is important for determining whether we are done. This is pretty straightforward part of the algorithm. Factors can be:

• Pre-defined number of generations
• Reaching desired value of a fitness function
• Convergence
Not improving by a significant ammount for given number of generations.

For our basic implementation we only simply check pre-defined number of generations (=iterations).

while (generation <= MAX_GENERATIONS) {
    /*
     * Main Algorithm Loop
     */ 
    generation++;
}

Specific problem: Optimization of an Airplane Design

Now that we've understood the basic principles behind the GA, let's try to apply it to a specific problem. Let's assume we want to optimize part of the design of an aircraft to maximize lift. We model this problem as having a few components for which we want to maximize the lift force. To limit the ranges of the components, we assume we are modeling this problem on an airliner (e.g. Boeing 777 and similar). Let's model the aspects of the problem onto the components of the algorithm now.

Population

Let's assume that each candidate solution (i.e., chromosome) in the population is represented by a vector $p = (V, S, \alpha , e, AR) \in \mathbb{R}^5$ of design variables (genes) that define a part of an aircraft. The dimensions correspond to:

• $V$ is the speed of the aircraft ($m/s$) $\in [50; 350]$
• $S$ is the wing area ($m^2$) $\in [60; 200]$
• $\alpha$ is the angle of attack (rad) $\in [0; 0.43]$
• $e$ is the Oswald efficiency factor $\in (0; 1]$
• $AR$ is the wing aspect ratio $\in [5; 15]$

Fitness function

Each chromosome is evaluated by a fitness function that computes its performance and assigns a fitness score. In this case we want to compute the maximum lift.

Lift ($L$): Lift is the force that holds an aircraft in the air. Lift generated by the plane depends on the air density, the speed of the aircraft, and the geometry of the wing. The lift can be computed (I hope - not an airplane eng ;)) using the following formula: $$ L = \frac{1}{2} \rho V^2 S \frac{(2 \pi \cdot \alpha)}{ (1 + (\pi \cdot e \cdot AR))} $$ where $\rho$ is the air density - assume constant at $1.293 kg/m^3$.

Parents Selection

We will choose two parents. Both as chromosome maximizing the fitness function among 10 randomly selected chromosomes. Randomness might make sense because for example of different conditions for the plane (meaning, the chromosome maximizing the fitness function might not maximize it in all conditions).

Selecting one parent will look like this:

Chromosome best = null;
for (int i = 0; i < 10; i++) {
    Chromosome individual = individuals[random.nextInt(individuals.length)];
    if (best == null || individual.getFitness() > best.getFitness()) {
        best = individual;
    }
}
return best;

Generating Children

We generate children as follows. To optimize but also to keep randomness in the process we randomly mix the genes of the two parents.

double[] childGenes = new double[genes.length];
double[] otherChildGenes = new double[genes.length];

for (int i = 0; i < childGenes.length; i++) {
    boolean mask = random.nextBoolean();
    if (mask) {
        childGenes[i] = this.getGenes()[i];
        otherChildGenes[i] = other.getGenes()[i];
    } else {
        childGenes[i] = other.getGenes()[i];
        otherChildGenes[i] = this.getGenes()[i];
    }
}

Chromosome first_child = new Chromosome(childGenes);
Chromosome second_child = new Chromosome(otherChildGenes);
Chromosome[] children = {first_child, second_child};

return children;

After we've performed the crossover, we will replace the worst children by the new offspring.

Stopping Criteria

We will pre-define the number of generations we want to optimize over and abort after achieving this number. We observe that in 9 from 10 runs, the algorithm converges around 75th generation/iteration, i.e. the algorithms settles on a final value at around 75th iteration. Other possibility would be to check the difference to a previous iteration and see how much of an improvement we made (check if we converged).

Sample Results

Following result was obtained by having POPULATION_SIZE = 150 and stopping criteria constant MAX_GENERATIONS = 100.

Generation: 1
Best fitness: 8121325.844336658
Generation: 2
Best fitness: 8121325.844336658
Generation: 3
Best fitness: 8121325.844336658
...
...
...
Generation: 73
Best fitness: 9273070.677375384
Generation: 74
Best fitness: 9273070.677375384
Generation: 75
Best fitness: 9273070.677375384
Generation: 76
Best fitness: 1.2647211860884406E7
...
...
Generation: 96
Best fitness: 1.2647211860884406E7
Generation: 97
Best fitness: 1.2647211860884406E7
Generation: 98
Best fitness: 1.2647211860884406E7
Generation: 99
Best fitness: 1.2647211860884406E7
Generation: 100
Best fitness: 1.2647211860884406E7

------Component--------|----Value----
Speed of the aircraift |   345.61
Wing area              |   189.95
Angle of attack        |     0.41
Oswald eff. factor     |     0.12
Wing aspect ratio      |     5.29

We can reason that the delievered result is somewhat reasonable by realizing that a loaded airplane can weigh up to $600.000 kg$ is corresponding to at least $6MN$ of needed lift. At generation 100, the best configuration has a lift force of roughly $9.5 MN$ (computed average of 10 simulations). Hence in the range of reasonable results. In real life achieving this lift by an airplane might be impossible (and maybe also unnecessary) - it's more about a half of our computed maximum for not so extremely heavy airplanes. Result is coming from simplifying and theoretizing about the components and their ranges.

How quickly this algorithm (in terms of generations) increases the maximum lift is visible from the following plot of average over 5 independent simulations.

See the complete implementation and two more similar examples on my GitHub.