Understanding & Implementing Dropout
Nov 26, 2023Overfitting is a known problem - it describes a scenario in which the model starts learning the data instead of the features of the data. To tackle this we can use regularization techniques like Weight Decay (adding a penalty term to the loss function, encouraging the model to prefer smaller weights), Early Stopping (terminating training before convergence) or... Dropout (randomly omitting some nodes in training process). Dropout helps to prevent overfitting and encourages the network to be more robust by preventing reliance on specific neurons. Dropout layers are layers in the neural net which are capable of omitting some number of connections from a node in the training process. These nodes are omitted with probability $p$ and kept with probability $1-p$. So if this probability $p=0.3$ we expect $70\%$ of the nodes present in the layer during training. In the inference, the nodes are always present. However, we compensate by multiplying the weights by the dropout probability $1-p$. The reason for this scaling is to ensure that the expected value of the output during inference remains approximately the same as during training.
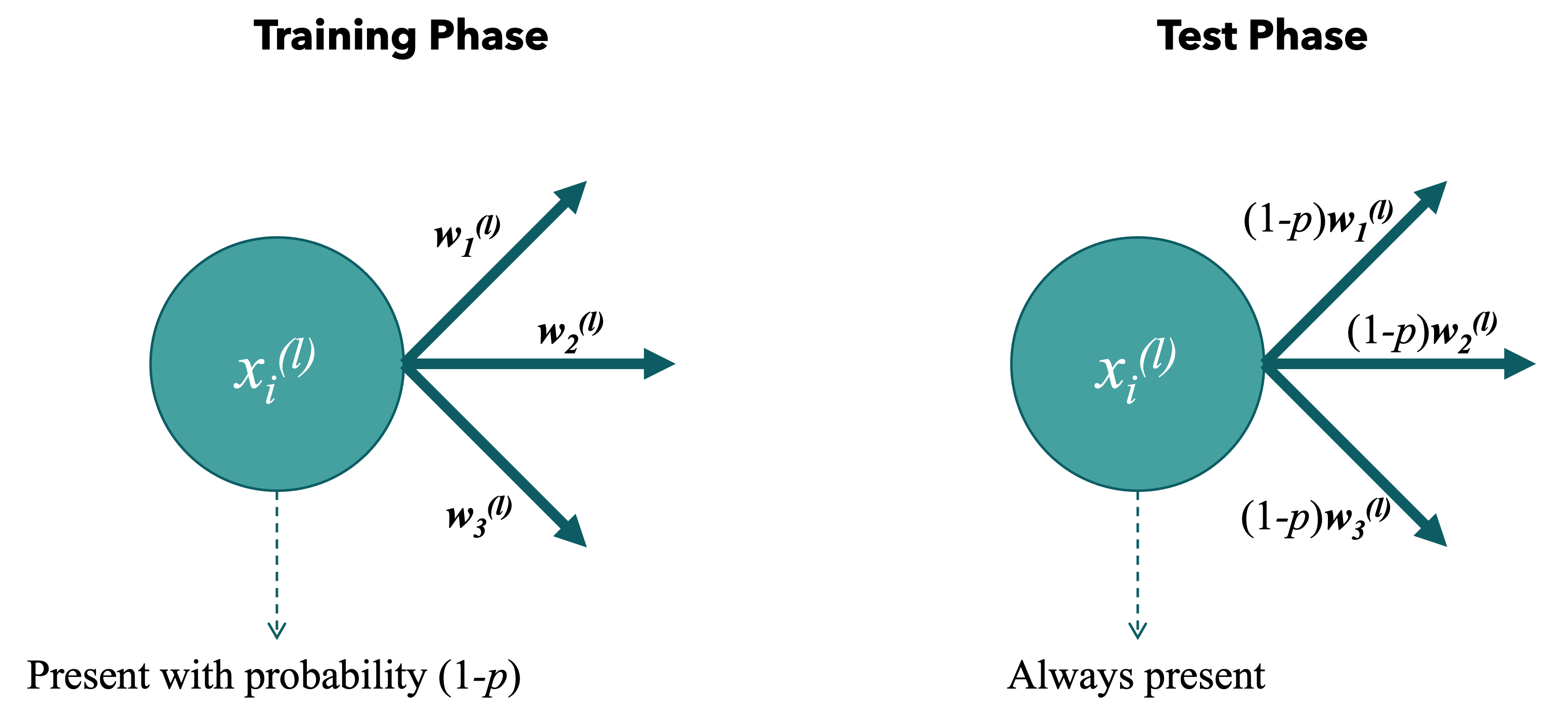 Training vs. Testing Phase
Training vs. Testing PhaseOf course, different nodes are dropped out in each iteration of forward pass. So in practice, it might look like something like the following animation. Here, we apply dropout on the very left layer with $p=0.33$. One frame of the animation is one forward pass.
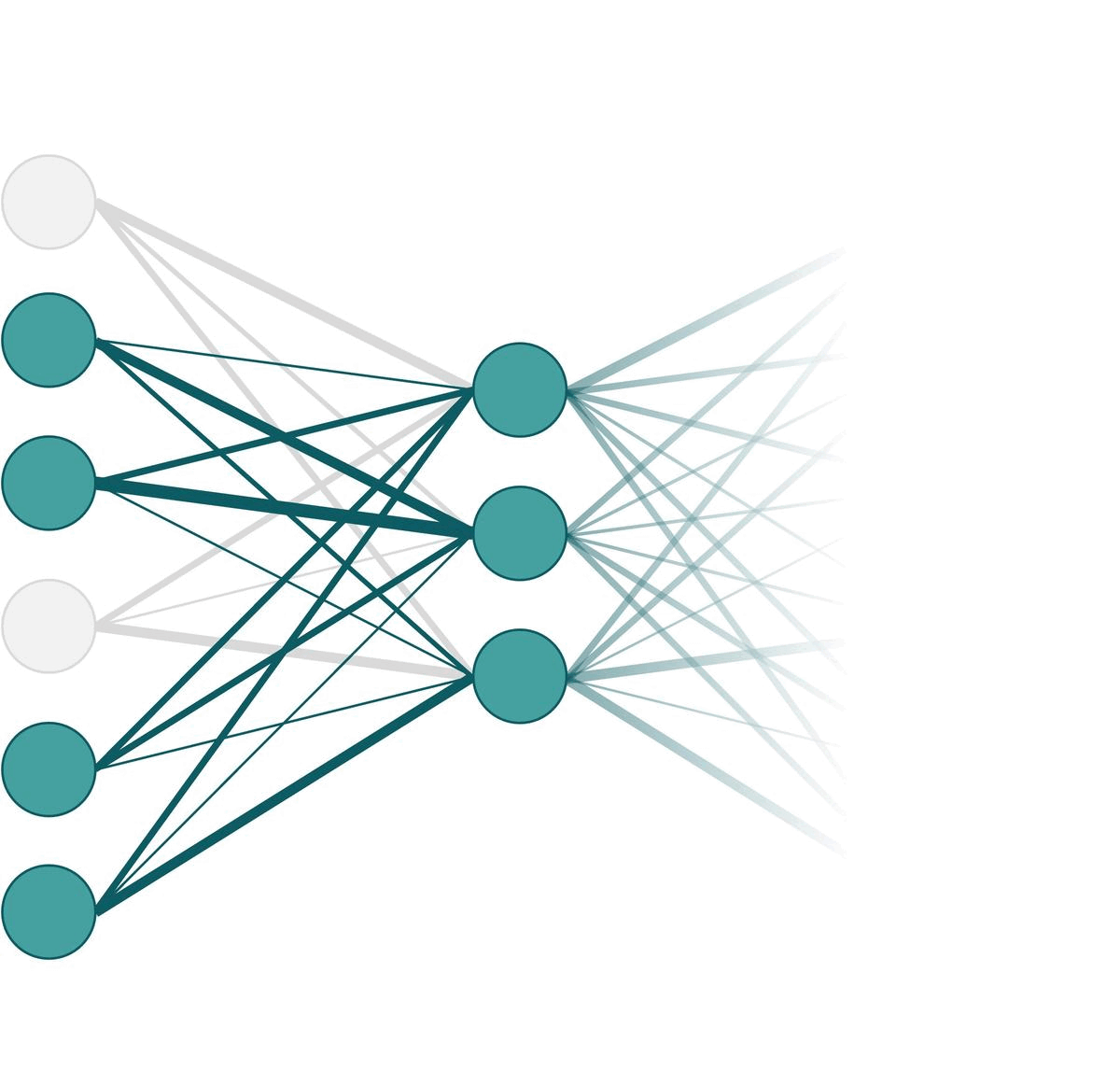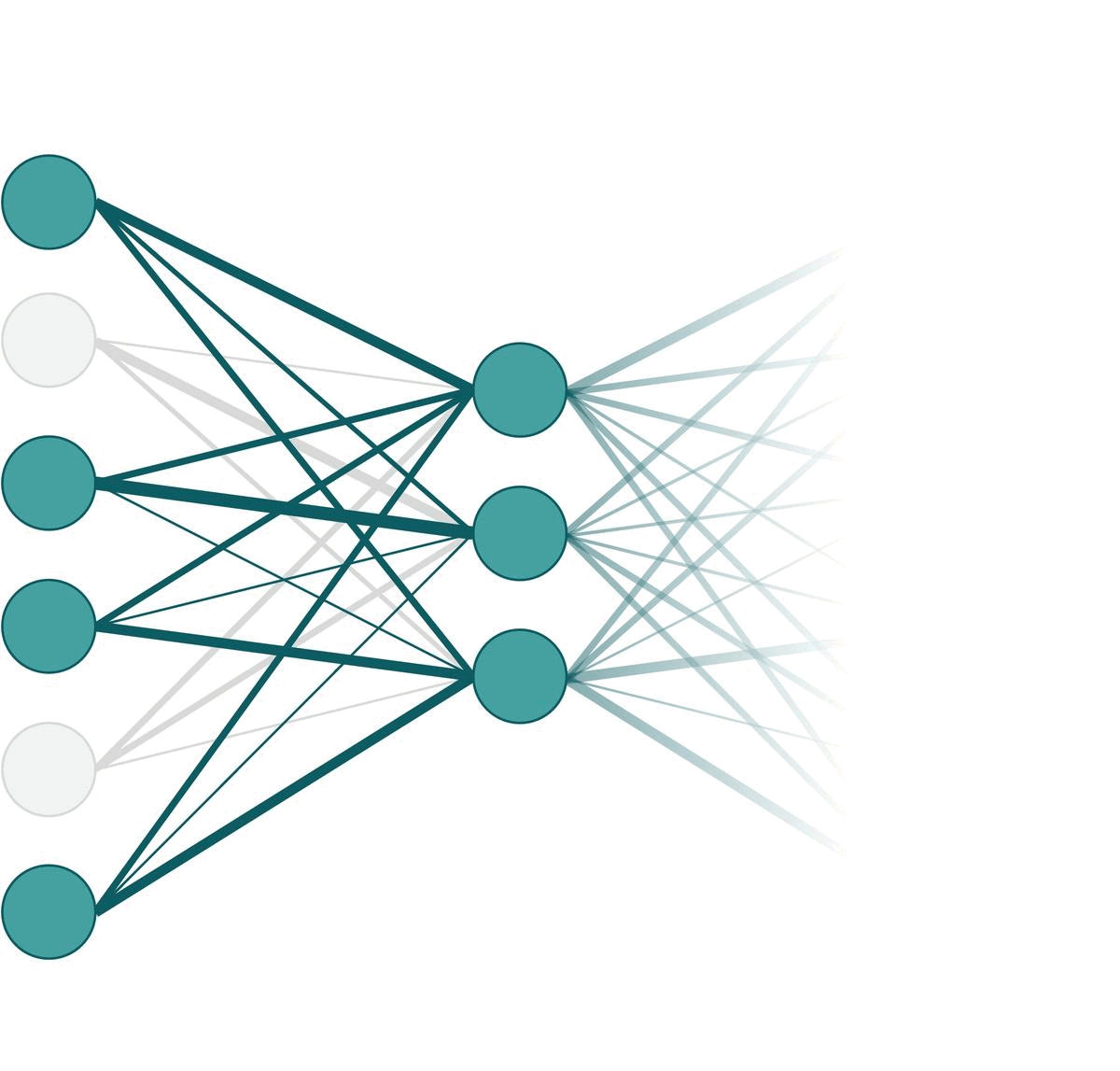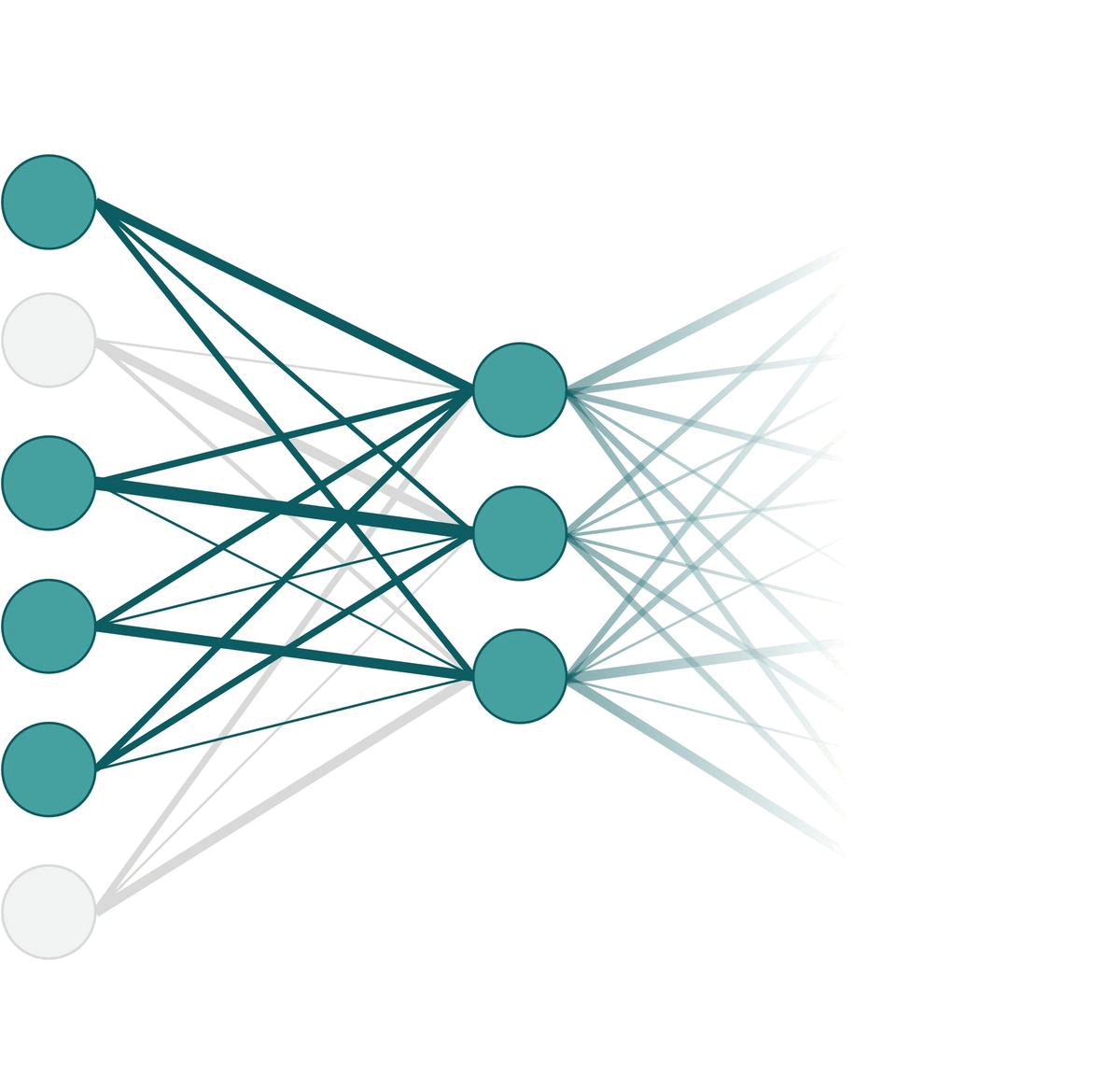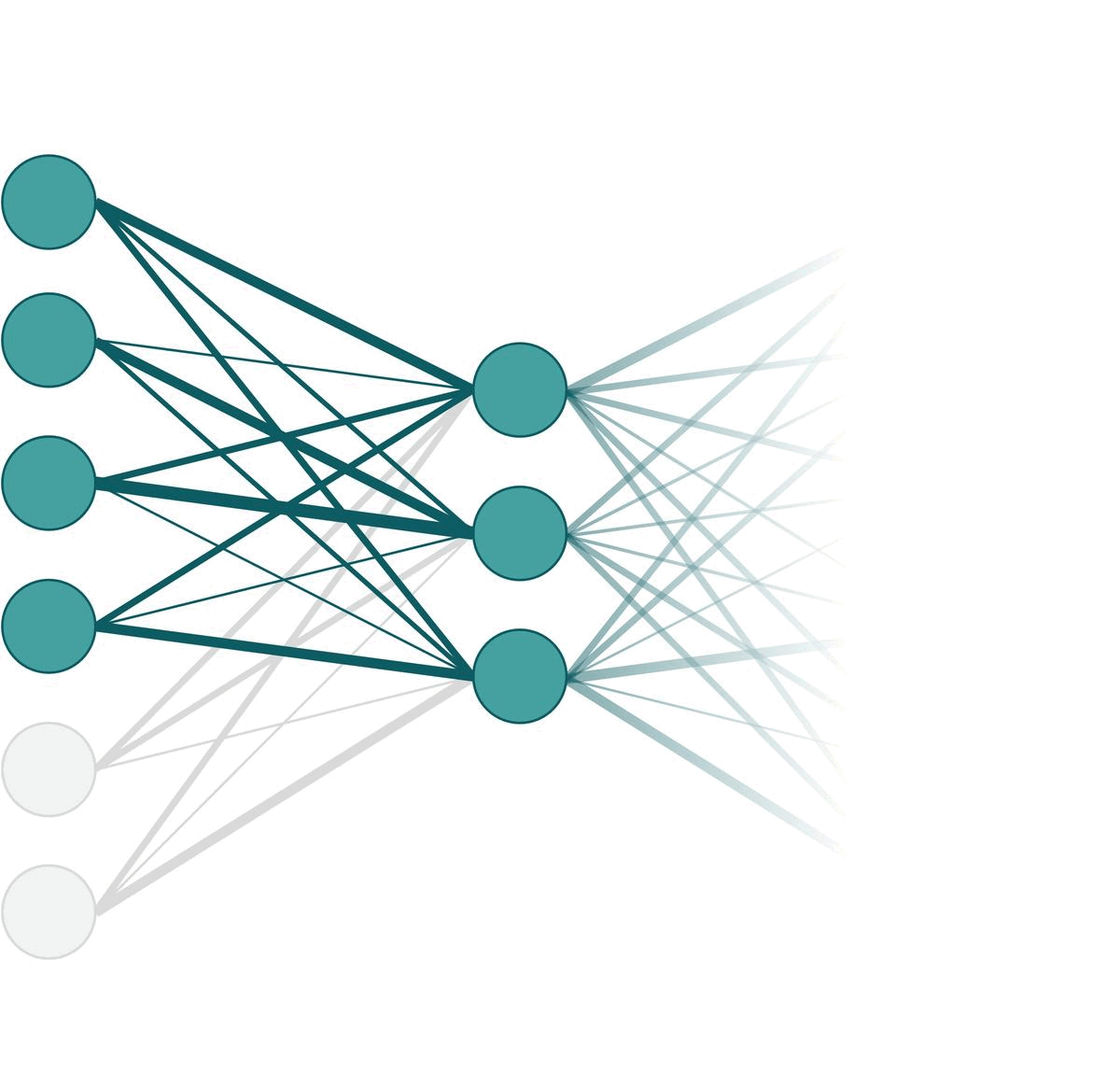 Different nodes can be omitted in each forward pass.
Different nodes can be omitted in each forward pass.
Using Dropout in PyTorch
When you use nn.Dropout in your model, it is added as a layer, and during training, it randomly zeros some of the elements in the input tensor with a probability specified by the p parameter. It can be used as follows in the code snippet. We define the dropout in __init__() and can then call it in the forward() of the model.
class MyModel(nn.Module):
def __init__(self):
# other activation functions definitions go here
self.dropout = nn.Dropout(p=0.5) # Defining the dropout with p = prob. that node is omitted
def forward(self, x):
x = torch.relu(self.fc1(x)) # Example Layer, fc1(x) is an activation function
x = self.dropout(x) # Calling the Dropout
x = self.fc2(x) # Example Layer 2, fc2() is an activation function
return x
#instatiate model
model = MyModel()
#train model hereUnder the Hood of Implementing Dropout
Let's go a step further and actually implement it. This way, there is no doubt about what Dropout actually does under the hood.
We said that dropout is essentially a layer that (literally) zeros out some of the values in the vector $X$ in a layer with probability $p$.
With that in mind we can define the dropout as subclass of nn.Module. By doing so, we gain all the functionality from nn.Module, which is a base class for all neural network modules in PyTorch. It provides a set of methods and attributes that are useful for building and managing neural network components. We have to (re-)define 2 functions from the parent class.
__init__(): This function is called when the class Dropout is initialized and the $p$ is stored.forward(): This function is called on the forward pass. Here, we define the behaviour on forward pass. This where we check the probability and either zero out or keep it.
class Dropout(nn.Module):
def __init__(self, p):
# to implement
def forward(self,X):
# to implementLet's start with the initialization. In the initialization we initialize the parent Module but also set the $p$ to be a known parameter. We naturally need to check if the given argument p is between 0 and 1.
def __init__(self, p):
super(Dropout, self).__init__() # ensuring parent-subclass logic is intact
if p < 0 or p > 1:
raise ValueError("Dropout probability must be between 0 and 1.")
self.p = p # storing the dropout parameterNow, we can define what happens on forward(). We said that this behaviour will be different based on whether we are in training phase or not. In training we want to return 0 with probability $p$ and if in inference mode we return $X$. Wait! But we said we have to scale-up the weights by $p$ for inference mode! True, but this can be accounted for already during training. The paper on Dropout says that another way to achieve the same effect is to scale up the activations by multiplying by $1/(1-p)$ at training time and not modifying the weights at test time. These methods are equivalent. This will make the implementation a little easier in that that with probability $1-p$ we don't only return $X_i$ but rather $\frac{x_i}{1-p}$ for each value in the input vector. For one value from the vector this would be:
$$
\text{Dropout}(x_i)=D_i \cdot x_i \cdot \frac{1}{1-p}=\left\{\begin{array}{cc}
x_i\cdot \frac{1}{1-p} & \text { if } D_i=1 \\
0 & \text { if } D_i=0
\end{array}\right.
$$
where $P\left(D_i=1\right)=1-p$ and therefore $P\left(D_i=0\right)=p$. It is clear that the random variable $D$ follows the $Ber(1-p)$ distribution and therefore for the input vector we want a [0/1] vector (let's call it a dropout mask) which follows $Bin(n, 1-p)$ where $n$ is the length of the vector. Generalizing for the whole input vector $X$, this is:
$$ \text{Dropout}\begin{align} ( [
x_{1},
x_{2},
\cdots
x_n ]^{\top} )
= \begin{bmatrix}
\text{Dropout}(x_{1}) \\
\text{Dropout}(x_{2}) \\
\vdots \\
\text{Dropout}(x_{n}) \\
\end{bmatrix} = \begin{bmatrix}
D_1 \cdot x_{1} \\
D_2 \cdot x_{2} \\
\vdots \\
D_n \cdot x_{n} \\
\end{bmatrix} \cdot \left ( \frac{1}{1-p} \right )\end{align} $$
Let's do everything again, but in code now. First, generating the dropout mask.
n = X.size() # size of the input vector
distribution = torch.distributions.binomial.Binomial(probs=1-self.p)
dropout_mask = distribution.sample(n) # create the mask based distribution of size nNow applying the dropout mask on the input and multiplying with $\frac{1}{1-p}$ as explained above.
X = X * dropout_mask * (1/(1-self.p))But we only want to do this in the training phase. To be able to differentiate between traning and test phase, we can use the variable training of the model and decide whether to do dropout based on it. We can switch between training/testing mode by calling model.train() and model.eval() respectively. We would then have something like:
if (self.training):
# all the code above to compute the dropout(X)
return X Putting it all together
class Dropout(nn.Module):
def __init__(self, p):
super(Dropout, self).__init__()
if p < 0 or p > 1:
raise ValueError("Dropout probability must be between 0 and 1.")
self.p = p
def forward(self,X):
if (self.training):
n = X.size()
distribution = torch.distributions.binomial.Binomial(probs=1-self.p)
dropout_mask = distribution.sample(n)
X = X * dropout_mask * (1/(1-self.p))
return X