Principal Component Analysis - Derived & Coded

Jul 7, 2023

Principal Component Analysis (PCA) is a method to get low dimensional representation of a high-dimensional dataset without losing the important features. PCA can be useful for visualization of the dataset or determining features from data. More formally, if we are given data set of $n$ original $d$-dimensional points $X = \{x_1,\dots,x_n\} \in \mathbb{R}^{n\times d}$, we want to obtain $n$ new $k$-dimensional points $Z = \{z_1, \dots, z_n\} \in \mathbb{R}^{n\times k}$ with $k\ll d$, for which the projection back onto the original dimension $d$ ($\bar X = \{\bar x_1,\dots,\bar x_n\} \in \mathbb{R}^{n\times d}$), is as close as possible to the original data $X$.

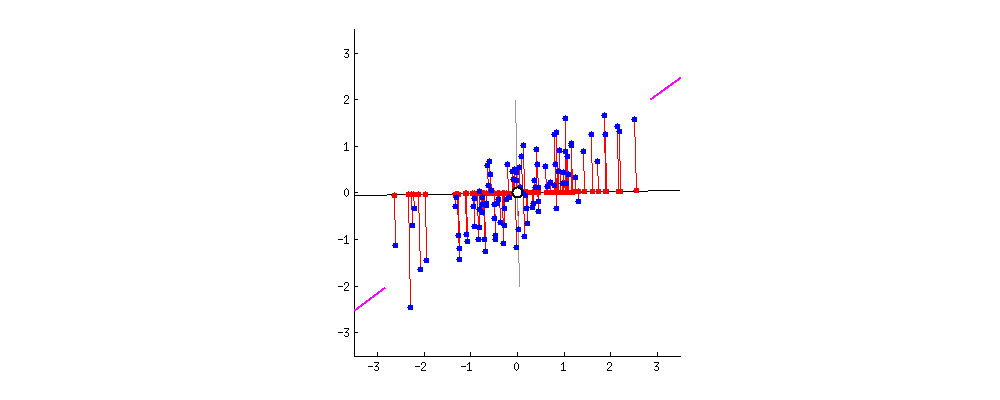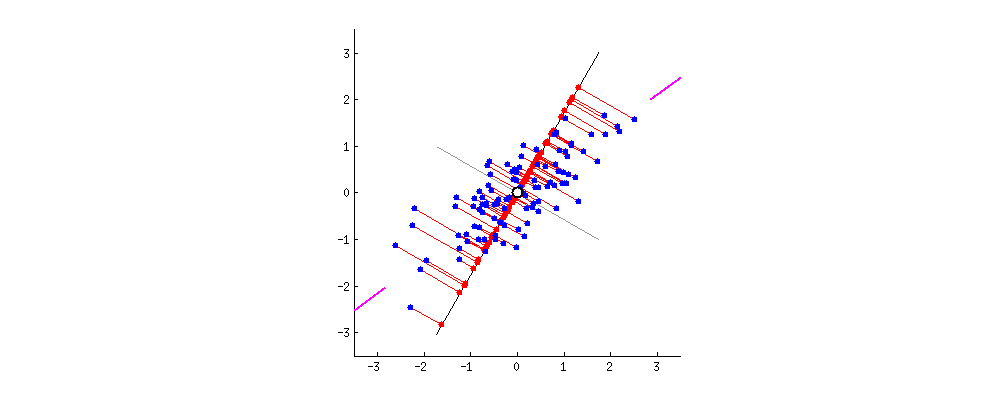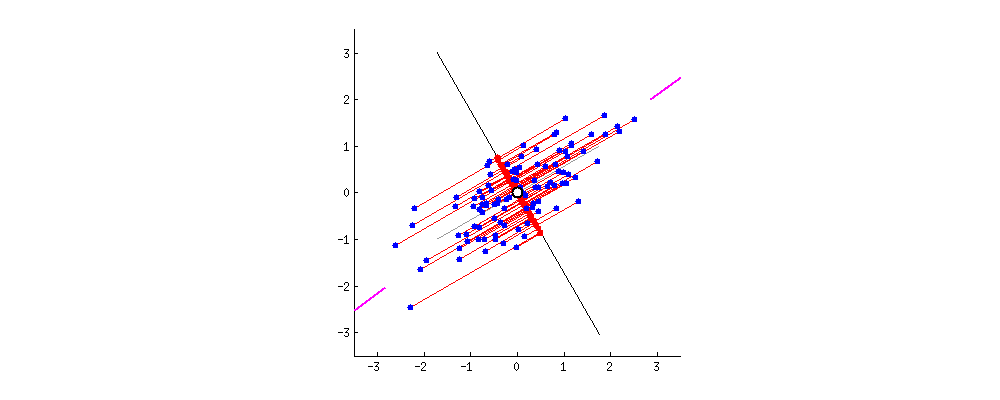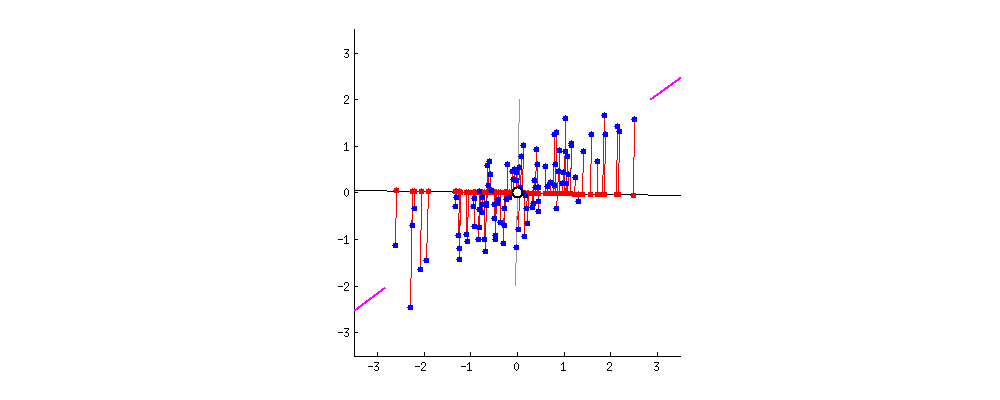Nice way of visualizing the distance
between $\bar X$ and $X$ [builtin.com]

For the next derivation, let's assume the data is standardized ($\iff$ mean $\mu$ = 0, standard deviation $\sigma$ = 1). We want to minimize $||\underbrace{{w}z_i }_{=\bar x_i} - x_i||_2^2$ for some vector $w$ (w.l.o.g., we assume $||w||_2 = 1$) and points $z_i$: $$ \left(\boldsymbol{w}^*, \mathbf{z}^*\right)=\arg \min _{\|\boldsymbol{w}\|_2=1, \mathbf{z}} \sum_{i=1}^n\left\| \boldsymbol{w}z_i-\boldsymbol{x}_i\right\|_2^2 $$ We assumed $||w||_2 = 1$, because for any fixed $||w||_2 = 1$ it holds that $z_i^* = \textbf{w}^Tx_i$. Our term is now therefore only minimizing over the $w$'s. We get $$ \begin{align} w^* &=\arg \min _{\|\boldsymbol{w}\|_2=1} \sum_{i=1}^n\left\| \boldsymbol{w}w^Tx_i-\boldsymbol{x}_i\right\|_2^2 \\ &= \arg \min_{\|w\|_2 = 1}\sum_{i=1}^n \|x_i\|_2 - \sum_{i=1}^n(w^\top x_i)^2 \\ &= \arg \max _{\|\boldsymbol{w}\|_2=1} \sum _{i=1}^n (w^Tx_i)^2 \\ &= \arg \max _{\|\boldsymbol{w}\|_2=1} w^T \Big( \underbrace{\sum _{i=1}^n x_i x_i^T}_{n\Sigma} \Big)w \\ \end{align} $$ where $\Sigma = \frac{1}{n}\sum_{i=1}^{n}x_ix_i^T$ is the covariance for $\mu = 0$ (data is centered). And now the optimal solution to $w^* =\arg \max _{\|\boldsymbol{w}\|_2=1} w^T \Sigma w$ is given by the principal eigenvector of $n\Sigma$. This means we can perform SVD decomposition the Covariance (or Correlation) matrix and extract the principal eigenvector (eigenvector corresponding to the highest eigenvalue).

SVD decomposition of matrix $A$ is a representation of that matrix as $$A = USV^\top$$ where $U,V$ are orthogonal matrices and $S$ is diagonal matrix with singular values. We can (together with eigenvectors) reorder them such that $\lambda_1 \geq \lambda_2 \geq \dots \lambda_d \geq 0$. That will be important for the next step.

Hence the SVD decomposition goes as follows. $$ n \Sigma={X}^T {X}={V} {S}^T \underbrace{{U}^T {U}}_{=I\ (\text{orthogonal})} {S} {V}^T={V} {S}^T {S} {V}^T={V} {D} {V}^T $$ And so (assuming the decreasing order of the eigenvalues) the solution is given by $v_1$ for $k=1$ - the first column of $V = \begin{pmatrix} v_1 | \dots |v_d \end{pmatrix}$ from the SVD, the eigenvector corresponding to the biggest eigenvalue. This is the vector carrying the most amount of information about the dataset.

In case of PCA for $k\geq1$, the problem generalizes into $$ (W^*,Z) = \arg\min_{W^\top W = I, Z} \sum_{i=1}^n \|Wz_i - x_i \|^2_2 $$ We can solve it analogously to $k=1$.
Obtaining $W$ - We can generalize the previous case for $k=1$ and say that the solution is given by $k$ eigenvectors corresponging the $k$ largest eigenvalues of the SVD decomposition on $X^\top X$, i.e. $$W = (v_1| \dots| v_k)$$ Obtaining $Z$ - As we already know how to get $z_i$ using $w$ from the $k=1$ case, it generalizes into $z_i = W^\top x_i$ for all $i=1,\dots ,n$, i.e. $$Z = W^\top \cdot X$$

Shortly summarized, we need to

Standardize the data
Compute the Covariance matrix of $X$
Decompose this matrix to get $k$ eigenvectors corresponding to the $k$ highest eigenvalues
Stack them vertically to get matrix $W = (v_1| \dots| v_k)$
Project the original data to obtain $ Z = (z_1,\dots,z_n)$

From scratch implementation

To make this implementation demonstration a little more robust, we will no longer assume standardized data. I will demonstrate each part of the implementation on an example. Let's say we want to perform PCA with $k=1$ onto a dataset $X$

Generating & Standardizing Dataset $X$

There are many datasets availbale for PC Analysis, but I thought it would be more fun to generate the data manually. The function generate_points_line() takes 4 arguments. min_x, max_x determine the range of x-axis, deviation allows the point to be a little further away from the $y=x$ line and the 2-dimensional point will be taken to the dataset with probability p.

def generate_points_line(min_x, max_x, deviation, p):
  points = list()
  for x in range(min_x, max_x+1):
      for y in range(min_x, max_x+1):
          if y < x+deviation and y > x-deviation:
              if (random.random() < p):
                  points.append((x,y))
  return points

X = generate_points_line(0,120,50,0.23)

Using the parameters min_x = 0, max_x = 120, deviation = 50 and p = .023, I generated the following dataset $X$.

Since we don't assume that $X$ is centered anymore, we have to standardize the data. This is nothing more than substracting the mean and dividing by the standard deviation of the dataset.

X = (X-np.mean(X, axis=0)) / np.std(X, axis=0) # standardize the data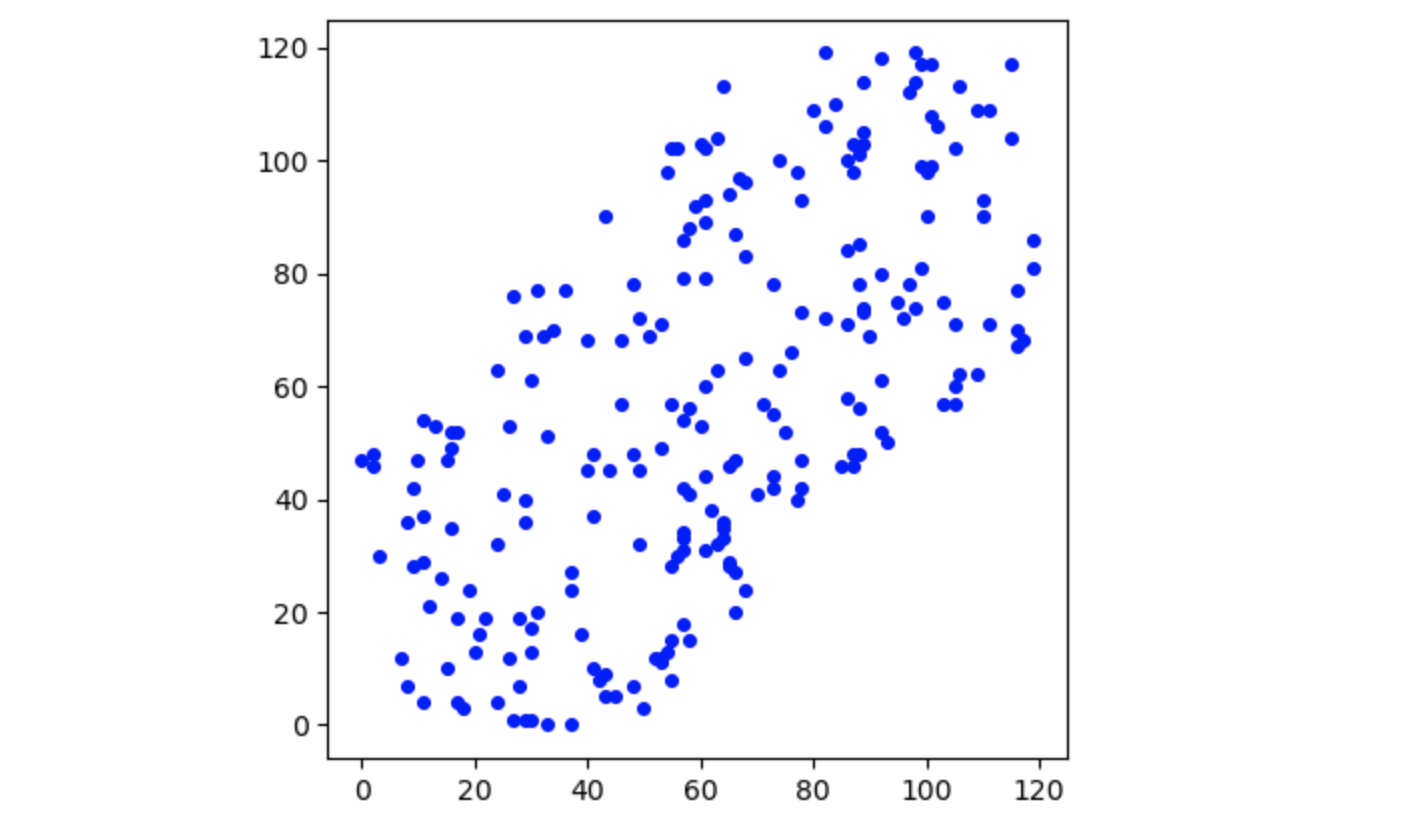

If we plot the data now, we notice that the plot looks exactly the same, only the axes shifted and the distance between points shrunk.

Generated Dataset

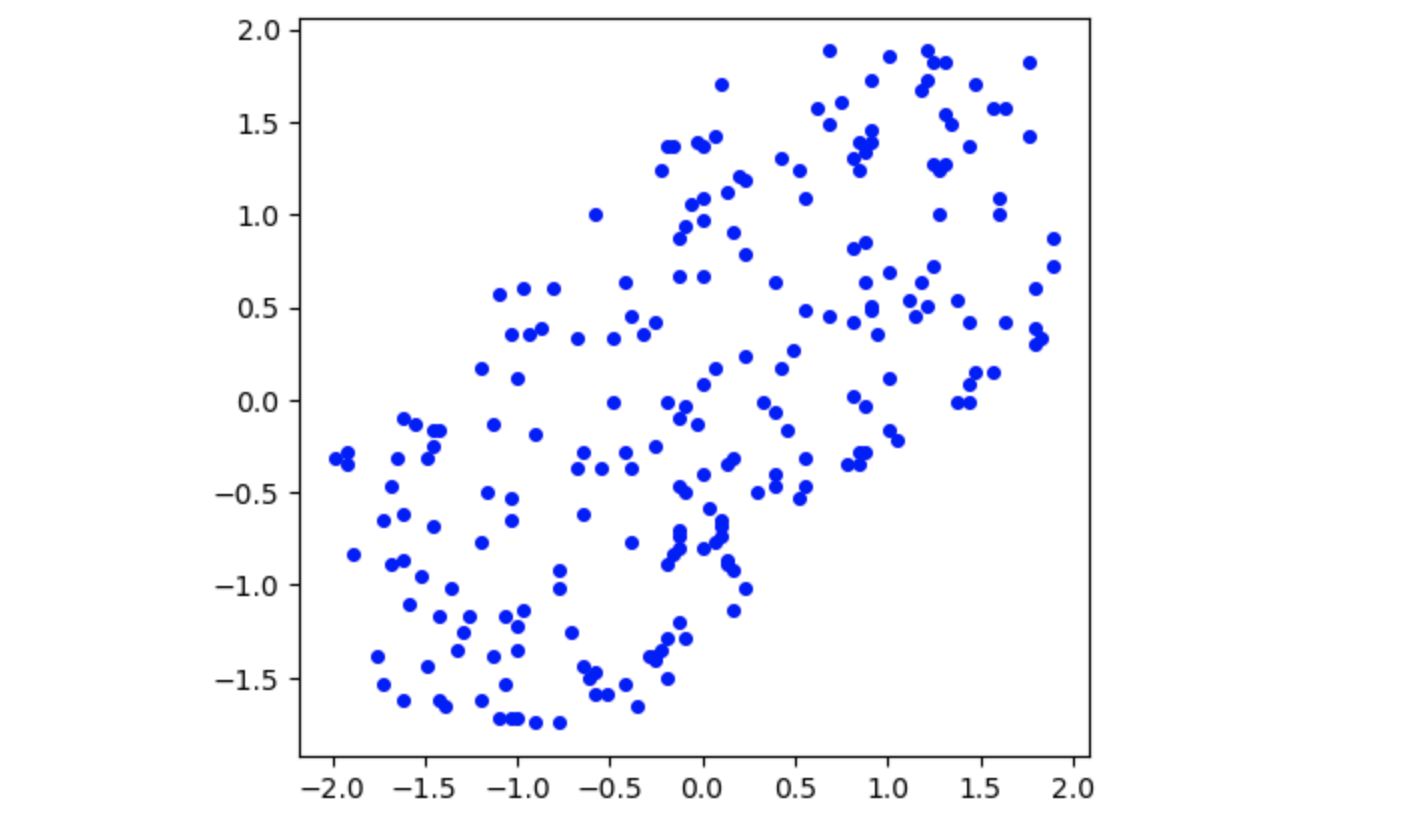Standardized Dataset

Covariance matrix

Computing the covariance matrix has now become easier since the $mean_X=0$ and $std_X=1$. All we need to do is $$ Cov = \frac{X^\top X}{n} \quad n=\text{number of points} $$

def cov_of_standardized(X):
  n = X.shape[0]
  return np.dot(X.T,X)/(n)

cov_X = cov_of_standardized(X)

For this particular dataset, the covariance matrix looks like this: $$ Cov_X = \begin{bmatrix} 1 & 0.62 \\ 0.62 & 1 \end{bmatrix} $$

This is not a suprising result as the covariance matrix of X is a square matrix where the diagonal elements are the variances of the variables. Since each standardized variable has a variance of 1, the diagonal elements of the covariance matrix of a standardized dataset are all 1.

Getting the Eigenvectors of the Covariance Matrix

Just for fun, let's see the eigenvalues (we expect two) and the corresponding eigenvectors (we expect 2x(1,2) vectors):

U,s,Vt = np.linalg.svd(cov_X) # https://numpy.org/doc/stable/reference/generated/numpy.linalg.svd.html
print(s)
print(U)

returns

[179.23427235  41.76572765] # eigenvalues
[[-0.70710678 -0.70710678]  # first eigenvector
 [-0.70710678  0.70710678]] # second eigenvector

It might be a little abstract what we just did, so let's look at the eigenvectors (these are the principal components) in the plane. They are scaled respectively to their eigenvalue. The blue vector is the [-0.70710678 0.70710678] component and the red one corresponds to the [-0.70710678 -0.70710678] component.

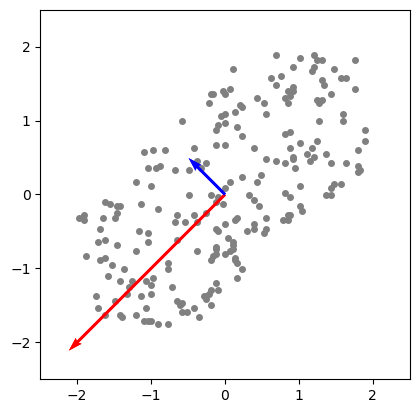PCA Components. Eigenvectors of the $Cov$ matrix scaled by their respective eigenvalue

As already described above, we're interested in extracting the k eigenvectors with the k largest corresponding eigenvalue. Since the $k=1$ here, we expect the max of both value (and hence its eigenvector [-0.70710678, -0.70710678] to be extracted). In the following snippet I implemented exactly that:

def k_most_eigenvectors(mat, k):
  u,s,vt = np.linalg.svd(mat) # https://numpy.org/doc/stable/reference/generated/numpy.linalg.svd.html
  indices = np.argsort(s) # returns indices from *smallest* to biggest EValue
  indices = np.flip(indices,0)[:k] # (data, axis) and up to k-th index
  W = np.real(u[:,indices]) # more context: https://numpy.org/doc/stable/reference/generated/numpy.linalg.svd.html
  return W

W = k_most_eigenvectors(cov, 1) # extract the 1 most significant eigenvector of the covariance of X
W

And indeed, what is returned is the expected eigenvector.

[-0.70710678, -0.70710678]

Mapping the data

Last think we have to do is map the old points and obtain the points: $Z = W^\top X$. Also remember that $\bar X = W\cdot Z$. This is simply:

def fit_pca(X, W):
  return np.dot(X,W)

Z = fit_pca(X,W)
X_bar = np.dot(W,Z.T)

And now we're done! We can plot the new points $(z_1, \dots, z_n)$ in orange against the original points in blue to visualize $Z$. We can do the same also with the re-projected points $(\bar x_1, \dots, \bar x_n)$ (distance of which from original dataset we wanted to minimize) and get a nice visualization of the dimension reduction.

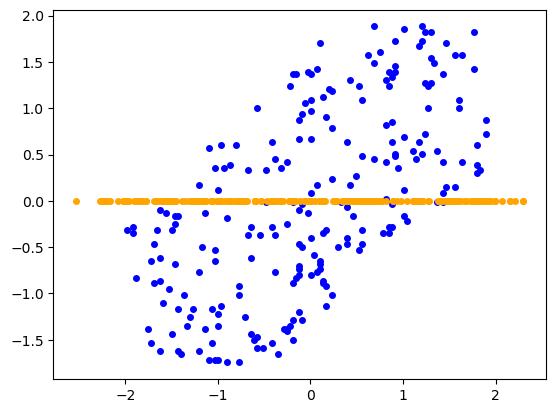Obtained dataset $Z$ - PCA on $X$ with $k=1$

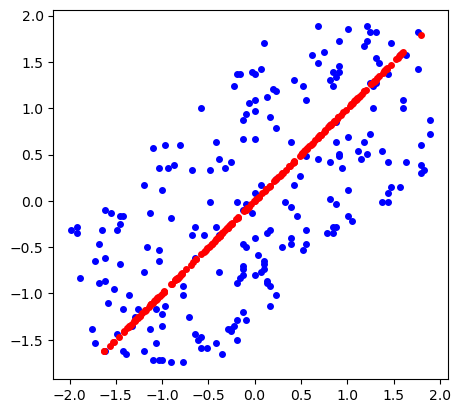Retrieved points $\bar X$