Using LSTM Recurrent Neural Networks to Predict Sepsis from Clinical Data Measurements
Mar 30, 2024Unlike traditional feedforward neural networks, which process fixed-size inputs independently, recurrent neural networks (RNNs) are designed to handle sequences of variable length. This makes them particularly useful for tasks involving time-series data or natural language processing. I have recently come across The PhysioNet/Computing in Cardiology Challenge 2019 where the goal is to come up with a model that is able predict the probability of sepsis (life-threatening condition that occurs when the body's response to infection causes organ failure, or death) based on the past clinical data measurements. We are given a time-series dataset of 20 thousand files containing hourly measurements of roughly 42 variables per patient. For purposes of this mini-project, we will try to predict the sepsis condition within the next hour based on past 10 hourly measurements. We have to preprocess the data, construct the dataset, design the model, train it and finally evaluate it. You can find the complete Jupyter notebook here.
Preprocessing the Data
Parsing the data. As said, we are given a little over 20.000 files of raw measurements. Each file corresponds to a single patient and it contains 42 variables measured over time. We want to convert these into a single pandas dataframe by looping over all the .psv files in the directory, read its content and save it into the dataframe we can later work with. We are adding an additional column with patient's ID so that we keep track of the origin of the data.
directory = "drive/MyDrive/EPOS/training_setA"
dfs = []
# Loop through each .psv file in the directory
for filename in os.listdir(directory):
if filename.endswith(".psv"):
file_path = os.path.join(directory, filename)
# Extract the patient id from the filename
patient_id = filename.split('.')[0]
# Read the .psv file into a DataFrame
df = pd.read_csv(file_path, sep='|')
# Add a column with patient's ID
df = df.assign(patient_id = patient_id)
# Append the DataFrame to the list
dfs.append(df)
# Concatenate all DataFrames into one
combined_df = pd.concat(dfs, ignore_index=True)
The combined_df now contains all the measurements in the dataset. We are dealing with 794400 rows x 42 columns. A lot. But not everythings is useful...
| # | HR | O2Sat | Temp | SBP | MAP | DBP | Resp | EtCO2 | BaseExcess | HCO3 | ... | Fibrinogen | Platelets | Age | Gender | Unit1 | Unit2 | HospAdmTime | ICULOS | SepsisLabel | patient_id |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | 69.11 | 1 | 0.0 | 1.0 | -44.60 | 1 | 0 | p019366 |
| 1 | 95.0 | 100.0 | 35.90 | 110.0 | 75.00 | 59.0 | 14.0 | NaN | NaN | NaN | ... | NaN | NaN | 69.11 | 1 | 0.0 | 1.0 | -44.60 | 2 | 0 | p019366 |
| 2 | 96.0 | 100.0 | 36.50 | 109.0 | 74.00 | 59.0 | 14.0 | NaN | 0.0 | NaN | ... | NaN | NaN | 69.11 | 1 | 0.0 | 1.0 | -44.60 | 3 | 0 | p019366 |
| 3 | 95.0 | NaN | 37.00 | 128.0 | 87.00 | 67.0 | 15.5 | NaN | 0.0 | NaN | ... | NaN | NaN | 69.11 | 1 | 0.0 | 1.0 | -44.60 | 4 | 0 | p019366 |
| 4 | 79.0 | 100.0 | 36.70 | 112.0 | 76.00 | 59.0 | 14.0 | NaN | -1.0 | NaN | ... | NaN | NaN | 69.11 | 1 | 0.0 | 1.0 | -44.60 | 5 | 0 | p019366 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 794395 | 71.0 | 96.0 | NaN | 108.0 | 66.67 | NaN | 26.0 | NaN | NaN | NaN | ... | NaN | NaN | 70.81 | 1 | 0.0 | 1.0 | -3.01 | 44 | 0 | p000434 |
| 794396 | 73.0 | 94.0 | 38.00 | 123.0 | 69.00 | NaN | 28.0 | NaN | NaN | NaN | ... | NaN | NaN | 70.81 | 1 | 0.0 | 1.0 | -3.01 | 45 | 0 | p000434 |
| 794397 | 75.0 | 97.0 | NaN | 125.0 | 71.00 | NaN | 23.0 | NaN | NaN | NaN | ... | NaN | NaN | 70.81 | 1 | 0.0 | 1.0 | -3.01 | 46 | 0 | p000434 |
| 794398 | 77.0 | 97.0 | NaN | 122.0 | 71.33 | NaN | 33.0 | NaN | NaN | NaN | ... | NaN | NaN | 70.81 | 1 | 0.0 | 1.0 | -3.01 | 47 | 0 | p000434 |
| 794399 | 78.0 | 97.0 | 37.11 | 125.0 | 70.33 | NaN | 24.0 | NaN | NaN | NaN | ... | NaN | NaN | 70.81 | 1 | 0.0 | 1.0 | -3.01 | 48 | 0 | p000434 |
We have to clean it up. It is worth looking at the features/columns of the dataframe and deciding whether it is useful or not. We can already see a lot of NaN values. Let's find out what percentage of each column is missing. Columns with a high percentage are most likely to be of small value to the dataset since they're not consistent.
stats = combined_df.isna().sum()/len(combined_df)
We get the following stats on missing values.
 Percentage of missing values in each column of the dataset
Percentage of missing values in each column of the dataset
As one can see some of the columns are just solely NaNs. Let's filter out data represented in a reasonable frequency. We can get rid of all the columns where more than 50% of the data is missing. Additionally, quick inspection of the features reveals the columns Unit1 and Unit2 are mutually exclusive and we can therefore omit them too.
const_vars = stats[stats<0.5].index # Choose columns with less than 50% of missing values
const_vars = const_vars.drop(["Unit1", "Unit2"]) # Drop Unit1 and Unit2
df_main = combined_df[const_vars] # Filter out the columns
We are now left with only 12 features instead of the original 42. This obviously hasn't solved the issue entirely but we now at least have a reasonable amount of data for each column. We still have features containing NaNs that need to fill them before constructing data training data sequences. Filling in should be probably done in isolation with respect to patients. I'm not sure how much sense it would make to interpolate outside of the single patient's scope. Same goes for later task of constructing the data sequences to the train the model. But first, let's normalize the data to improve convergence speed, and generalization. We want to apply min-max normalization to df_main (excluding the "patient_id" column) to scales the numerical features to a range between 0 and 1.
norm = (df_main.loc[:, df_main.columns != "patient_id"]-df_main.loc[:, df_main.columns != "patient_id"].min())/(df_main.loc[:, df_main.columns != "patient_id"].max()-df_main.loc[:, df_main.columns != "patient_id"].min())
df_main[norm.columns] = normFilling the missing values. Keeping things simple - I will use pandas.DataFrame.interpolate - the defualt linear interpolation treats the values as equally spaced. Though this fills most of the NaN in each dataframe per patient, it can still happen that we encounter some NaN values. The interpolation sometimes doesn't work - if there is no value present within the column in the dataframe, there is nothing to interpolate. In that case we are left with NaN column. If we detect those, we just omit the particular sequence and don't add it to our dataset.
Constructing the dataset. We want to train in the following manner: Given the past 10 hrs of recorded clinical data, is it likely that the patient will suffer from sepsis in the next hour? This means we take slices/sequences of length 10 (our context length so to say) and look at the ground truth; the SepsisLabel of the next hour. This will be then fed into many-to-one LSTM RNN.
 Constructing the dataset out of the big all-in-one dataframe
Constructing the dataset out of the big all-in-one dataframe
grouped_by_patients = df_main.groupby("patient_id")
all_windows = [] # Store the created time windows here
for pid, data in grouped_by_patients: # Loop over each of the patients
data = data.interpolate() # Impute missing values within a patient's scope
cutoff = len(data) # Get number of measurements for the patient
context_length = 10 # Define the length of each sequence
i = 0
while (i+context_length + 2 < cutoff): # Loop over the patient's measurements
end = i+context_length+1
i+=1
# Take the 10 measurements and drop the patient_id column
window_data = data.iloc[i:end].drop(columns = ["patient_id"])
# If there are NaN values in the window, skip it
if np.isnan(window_data).any().any(): continue
x_data = window_data.values # Convert to numpy array
y_label = int(data.iloc[end+1]["SepsisLabel"]) # Get the label for the next hour
patient = {"X": x_data, "y": y_label} # Store the sequence and the label
all_windows.append(patient) # Append to the list of all sequences
count += 1
# Transform "X" column into numpy array
X = np.array(pd.DataFrame(all_windows)["X"]))
# Cat the correctly shaped tensors
X = np.concatenate(X.reshape((len(all_windows), 10, 11))
# Transform ground y into numpy array
y = np.array(pd.DataFrame(all_windows)["y"])
Now we have our X and y and all that needs to be done is split the dataset into test and training sets. We want to allocate 80% for training and 20% for testing the performance.
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# To PyTorch tensors
X_train_tensor = torch.tensor(X_train, dtype=torch.float32).to(device)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32).to(device)
X_test_tensor = torch.tensor(X_test, dtype=torch.float32).to(device)
y_test_tensor = torch.tensor(y_test, dtype=torch.float32).to(device)
# Create a TensorDataset
train_dataset = TensorDataset(X_train_tensor, y_train_tensor)
test_dataset = TensorDataset(X_test_tensor, y_test_tensor)
# Define batch size and create DataLoader instances for training and testing subsets
batch_size = 64
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
Preparing the Model
It seems like a good idea to use a bidirectional LSTM (Long Short-Term Memory) neural network followed by fully connected (dense) layers. Bidirectional LSTMs are capable of capturing both past and future context from sequential data, which will be useful in this setting.LSTM networks are good in modeling temporal dependencies in sequential data and capturing patterns in the data sequences. Since we are taking last 10 hours and predicting the next one, we only care about the last piece of the output. This is called many-to-one RNN. In a Many-to-One RNN, multiple input time steps are processed to produce a single output. This output is typically produced by the final time step of the recurrent layer.
 Many-to-one recurrent neural networks by chopping off all except for last
Many-to-one recurrent neural networks by chopping off all except for last
Model Summary. The model takes the input sequence and sends it through two bidirectional LSTM layers. Using two bidirectional layers instead of one can help capture more complex dependencies within the input sequence. We are using dropout of 0.2. The output of the LSTM has shape of (batch_size, sequence_length, 2*hidden_size). We use 124 hidden units and batch size of 64. The output of the LSTM layer is passed through three fully connected layers with 248 - 124 - 32 hidden units and ReLU activation functions. The final layer is a single neuron with a sigmoid activation function. The model is trained using binary cross-entropy loss and the Adam optimizer.
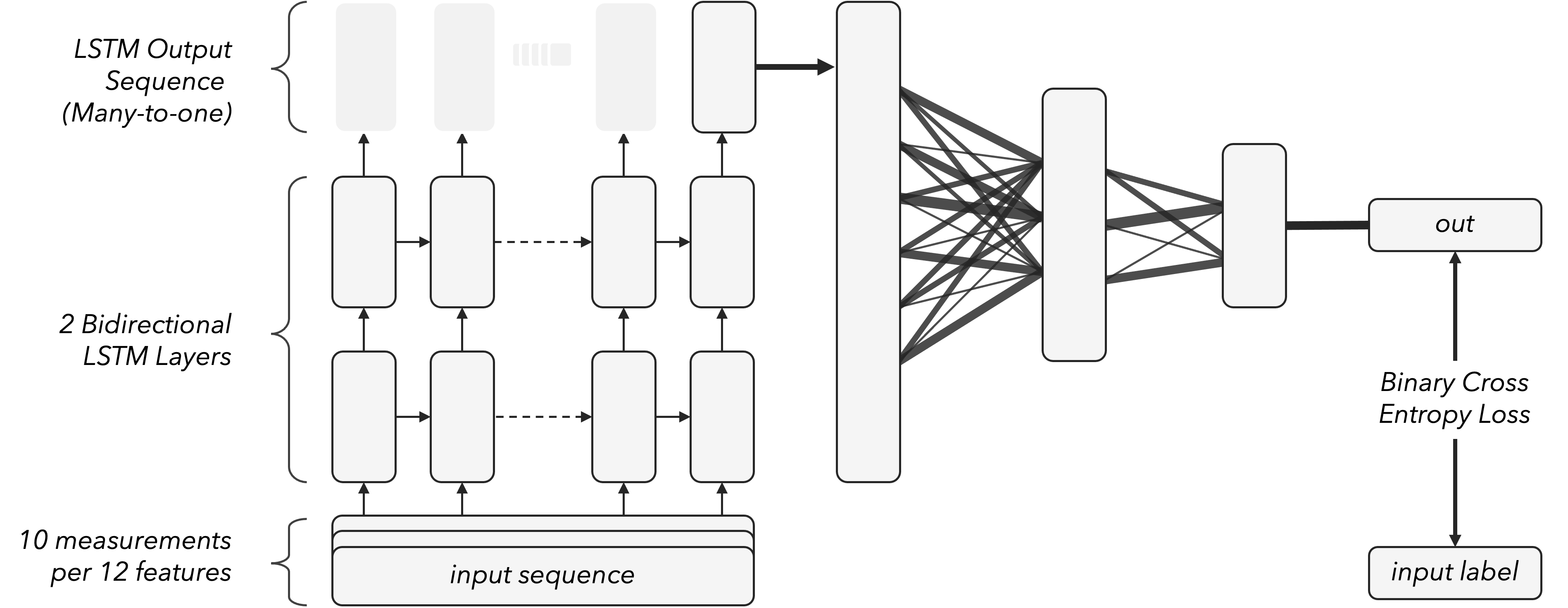 Visualization of the model used
Visualization of the model used
In RNNs, we have states. A "state" refers to the internal representation of the network's memory at a particular time step. It contains a representation of information about the current input and the context from previous time steps. This state evolves over time as the network processes each element in the input sequence. For us, it is only important that we have to initialize them (randomly) when we call the LSTM on the input sequence. The LSTM returns a tuple of (output_sequence, states). We can just ignore the states on output. There are not relevant for the predictions. Let's specify the model in code:
class LSTMModel(nn.Module):
def __init__(self, input_size, hidden_size, num_layers):
# Initialize
super(LSTMModel, self).__init__()
# Double bidirectional LSTM RNN layer
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, dropout=0.2, bidirectional=True)
# Dense hidden
self.fc1 = nn.Linear(2*hidden_size, hidden_size)
self.fc2 = nn.Linear(hidden_size, 32)
self.fc3 = nn.Linear(32,1)
# Activations
self.relu = nn.ReLU()
self.sigmoid = nn.Sigmoid()
def forward(self, x):
# Initialize hidden state and cell state with zeros
h0 = c0 = torch.zeros(2*self.num_layers, x.size(1), self.hidden_size).to(x.device)
initial_state = (h0, c0)
out, _ = self.lstm(x, initial_state) # Shape (10, 2*hidden_size)
out = out[:, -1, :] # Cutoff the last sequence: many-to-one (batch, 1, 2*hidden_size)
out = self.relu(self.fc1(out)) # Send through first hidden layer + ReLU
out = self.relu(self.fc2(out)) # Send through second hidden layer + ReLU
out = self.sigmoid(self.fc3(out)) # Send through final hidden layer + Sigmoid $\in [0,1]$
return out
I have additionally defined a train function and can now train the model by defining training parameters and calling the training function.
input_size = X_train.shape[2] # Number of features per time step
hidden_size = 124
num_layers = 2
model = LSTMModel(input_size, hidden_size, num_layers).to(device)
# Initialize the model, loss function, and optimizer
criterion = nn.BCELoss() # binary cross entropy loss
optimizer = torch.optim.Adam(model.parameters(), lr=0.01) # experiment here with learning rate
train_model(model,train_loader, criterion, optimizer, 3, batch_size)
The model seems to be doing very well during training as we have Loss: 0.0313, Accuracy: 0.9748 in the last epoch. Let's see the ROC curve on the test set.
# Test the model on test set (20% of dataset)
y, scores = test_model(model, test_loader)
fpr, tpr, thresholds = metrics.roc_curve(y, scores)
Plotting tpr (True Positive Rate) against fpr (False Positive Rate) will show us the ROC curve. Each point on the curve represents a different threshold setting used to classify the positive and negative classes.
A diagonal line from the bottom left to the top right (the "random classifier line") would represent the performance of a random classifier with an Area Under the Curve (AUC) of 0.5.
The higher the ROC curve lies above the random classifier line, the better the model's performance. An ROC curve that hugs the top-left corner of the plot indicates a model with high sensitivity (TPR) and
low fall-out (FPR) across a range of threshold values.
 AUC of the ROC shows how well the model performs
AUC of the ROC shows how well the model performs
For this model, we get AUC of 0.94 on the test set. That sounds great, but there is a catch. The dataset is highly imbalanced.
print((len(y[y == 1]) / len(y))*100)
>>> 2.6776165515784474
The sepsis condition is rare and only 2.6% of the testset patients have it.
This means that the model could achieve a high accuracy by simply predicting that no patient has sepsis. Also the ROC curves are insensitive to these imbalances and can be very misleading. They can give a false
impression of good performance because they mainly focus on true positive
rate and false positive rate without considering the class distribution.
On the other hand, F1 score gives more of a balanced view of the model's performance.
$$
F_1:=\frac{2 \mathrm{TP}}{2 \mathrm{TP}+\mathrm{FP}+\mathrm{FN}} .
$$
In our imbalanced dataset, correctly identifying instances of the minority class (true positives in our case) is crucial.
The F1 score, by considering both precision (= true_positives / true_positives + false_positives) and recall (= true_positives / true_positives + false_negatives), provides a measure of how well the
classifier is performing in terms of capturing these true positives. This is a more reliable metric in scenarios like this.
print(metrics.f1_score(y, scores.round(0)))
>>> 0.8875479978058146